فیلترهای کم گذر رونمایی شدند: یک راهنمای جامع برای عملکرد و تأثیر آنها
پیشرفت فیلترهای کم گذر نشان دهنده یک قدم مهم در زمینه الکترونیک و مهندسی صوتی است و امکان دستکاری دقیق و پیشرفت پاسخ های فرکانس را در تعداد بیشماری از برنامه ها فراهم می کند.این فیلترها ، چه القایی ، خازنی و چه یکپارچه سازی پیشرفته از اجزای سازنده ، به عنوان ابزاری جدی در کاهش نویزهای با فرکانس بالا ناخواسته در حالی که حفظ فرکانس های کمتری دارند ، خدمت می کنند.جوهر فناوری فیلتر کم گذر در توانایی تبعیض در برابر فرکانس ها نهفته است ، ویژگی ای که در بخش های مختلف اعم از مدار الکترونیکی پیشرفته گرفته تا محیط های تولید صوتی ظریف است.این مقاله با کاوش در مکانیک فنی فیلترهای مختلف کم گذر ، از جمله ساخت آنها ، اصول عملیاتی و زیربنای ریاضی از طریق عملکردهای انتقال ، طیف گسترده ای از برنامه های فیلتر کم گذر و تأثیر عمیق آنها در بهبود عملکرد سیستم ، یکپارچگی سیگنال را بررسی می کند.، و زیبایی شناسی شنوایی.
کاتالوگ
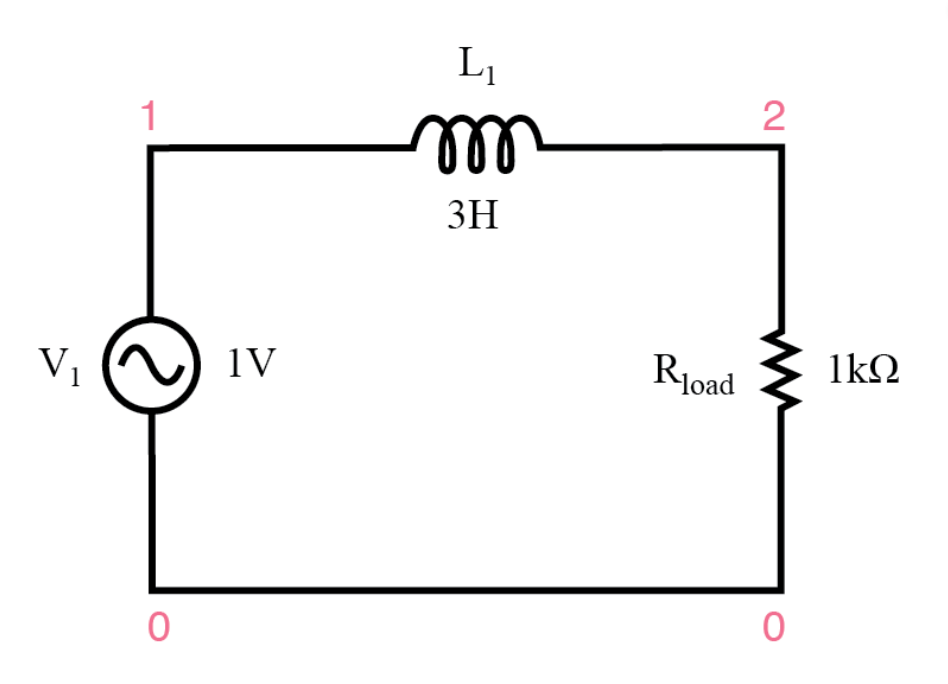
شکل 1: فیلترهای کم گذر القایی
مکانیک فیلترهای کم گذر القایی
فیلترهای کم گذر القایی برای مدیریت توزیع فرکانس در مدارها مورد نیاز است.آنها در کاهش سیگنال های با فرکانس بالا بسیار مؤثر هستند در حالی که اجازه می دهند فرکانس های کمتری از آن عبور کنند.مؤلفه اصلی این فیلترها سلف است که با افزایش فرکانس سیگنال امپدانس خود را افزایش می دهد.این ویژگی به سلف اجازه می دهد تا مانند یک مقاومت وابسته به فرکانس عمل کند و مقاومت در فرکانس های بالاتر را افزایش دهد.
امپدانس یک سلف قابل بیان است 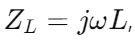 ، فرکانس زاویه ای کجاست و
، فرکانس زاویه ای کجاست و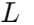 القاء استبه عنوان فرکانس زاویه ای
القاء استبه عنوان فرکانس زاویه ای 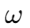 امپدانس نیز افزایش می یابد و باعث می شود که در مسدود کردن فرکانس های بالا بهتر شود.برعکس ، در فرکانس های پایین تر ، امپدانس کم است و به این سیگنال ها اجازه می دهد به راحتی از آن عبور کنند.
امپدانس نیز افزایش می یابد و باعث می شود که در مسدود کردن فرکانس های بالا بهتر شود.برعکس ، در فرکانس های پایین تر ، امپدانس کم است و به این سیگنال ها اجازه می دهد به راحتی از آن عبور کنند.
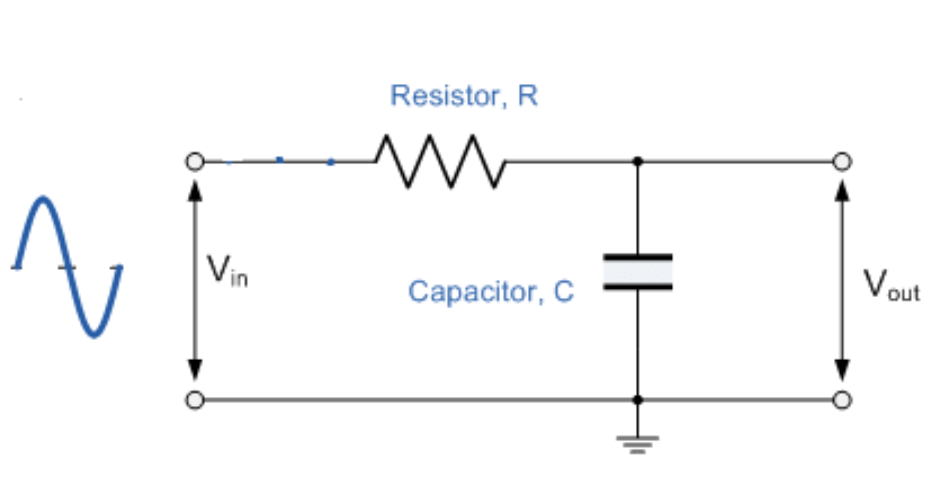
شکل 2: فیلترهای کم عبور خازنی
ویژگی های فیلترهای کم عبور خازنی
فیلترهای کم عبور خازنی از خواص منحصر به فرد خازن ها استفاده می کنند ، که با افزایش فرکانس سیگنال ، امپدانس کاهش را نشان می دهند.این فیلترها با قرار دادن خازن به موازات بار ، مسیری را ایجاد می کنند که سیگنال های با فرکانس بالا را به دور از خروجی منحرف می کند.فرکانسهای بالا سپس توسط یک مقاومت واسطه ای ، معروف به R1 ، جذب می شوند که آنها را از فیلترهای کم گذر القایی جدا می کند.
این فیلتر به طور معمول فقط از یک خازن و یک مقاومت تشکیل شده است و آن را ساده و در عین حال بسیار مؤثر می کند.خازن ها در برابر موضوعاتی مانند اتصال القایی و اتلاف انرژی قوی هستند.بر خلاف سلف ، که به دلیل آرایش و مواد فیزیکی آنها از تلفات مقاومت و مغناطیسی رنج می برند ، خازن ها عملکرد پایدار و قابل پیش بینی را حفظ می کنند.سلف ها به دلیل مقاومت در برابر سیم و هیسترزیس مغناطیسی ، راندمان را از دست می دهند ، مشکلاتی که خازن ها با آن روبرو نیستند و منجر به پاسخ خطی تر و قابل اعتماد تر در شرایط مختلف می شوند.
فیلترهای خازنی به ویژه در برنامه هایی که نیاز به عملکرد مداوم دارند ، مانند تجهیزات صوتی یا دستگاه های پردازش سیگنال ، که در آن یکپارچگی سیگنال مهم است ، مفید هستند.در حالی که فیلترهای خازنی در بسیاری از کاربردهای الکترونیکی به طور گسترده ای ترجیح داده می شوند ، فیلترهای القایی هنوز هم در زمینه های خاص نقش اساسی دارند.به عنوان مثال ، در مدارهای منبع تغذیه AC-DC ، به دلیل حداقل مقاومت در برابر سری ، فیلترهای القایی مورد نیاز است ، با وجود ناکارآمدی آنها ، از بین رفتن قدرت پایین تر و راندمان بهتر اطمینان می یابد.
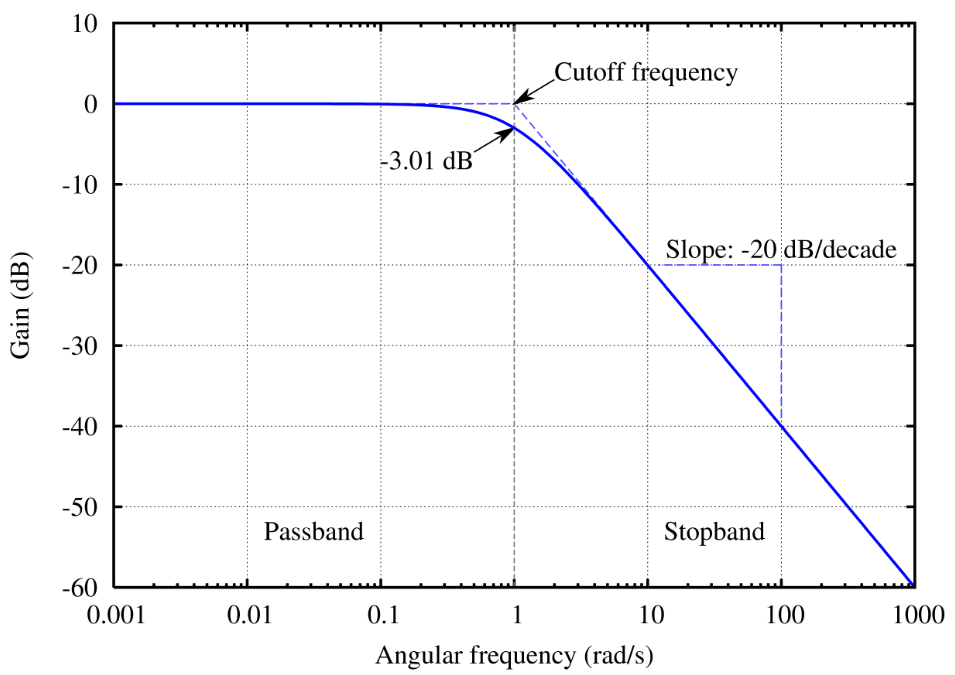
شکل 3: فرکانس برش
نقش فرکانس برش در فیلترهای الکترونیکی
فرکانس برش در طراحی فیلتر کم گذر قرار می گیرد و نقطه ای را نشان می دهد که فیلتر شروع به کاهش چشمگیر سیگنال ورودی می کند.از نظر فنی ، آن را به عنوان فرکانس تعریف می کند که ولتاژ خروجی به 70.7 ٪ از مقدار ورودی آن کاهش می یابد ، مطابق با کاهش -3 dB در مقیاس لگاریتمی ، که نشانگر نصف قدرت است.پارامترهای کلیدی مانند مقاومت و خازن این فرکانس را در فیلترهای کم گذر مقاوم در برابر خازنی تعیین می کنند.
برای محاسبه فرکانس برش ، واکنش خازنی را برابر با مقاومت تنظیم می کنید.فرمول است 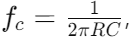 ، کجاست
، کجاست 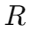 مقاومت ،
مقاومت ، ظرفیت است ، و
ظرفیت است ، و فرکانس برش است.این محاسبه شرایط ایده آل را فرض می کند ، اما عملکرد دنیای واقعی اغلب به دلیل عواملی مانند تغییر در مقاومت بار و ماهیت غیر ایده آل ، از جمله خازن های انگلی و القایی که در طراحی اولیه در نظر گرفته نشده است ، منحرف می شود.
فرکانس برش است.این محاسبه شرایط ایده آل را فرض می کند ، اما عملکرد دنیای واقعی اغلب به دلیل عواملی مانند تغییر در مقاومت بار و ماهیت غیر ایده آل ، از جمله خازن های انگلی و القایی که در طراحی اولیه در نظر گرفته نشده است ، منحرف می شود.
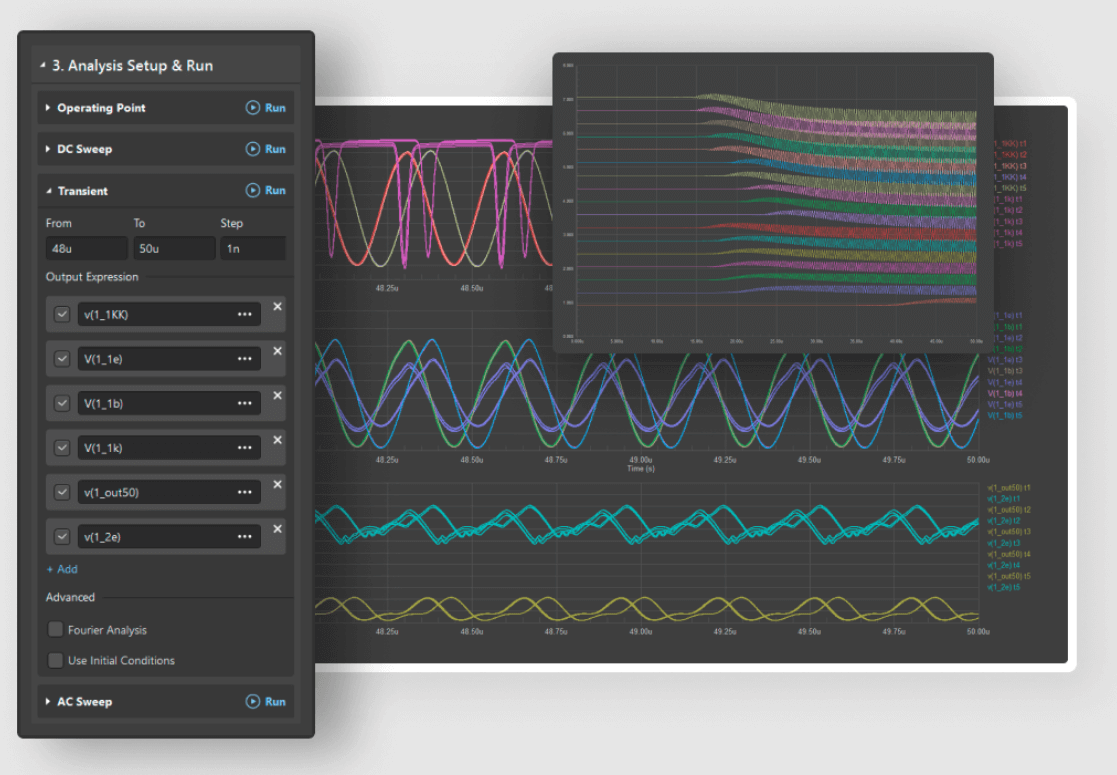
شکل 4: شبیه سازی ادویه
برای پرداختن به این اختلافات ، طراحان از شبیه سازی های ادویه ای برای مدل سازی فیلترها در شرایط واقع گرایانه استفاده می کنند.این شبیه سازی ها به تنظیم پویا پارامترها اجازه می دهند تا با نتایج مورد نظر تراز شوند.همچنین درک چگونگی عملکرد فرکانس برش در متن یک مدار نیز قابل توجه است.عواملی مانند دما و رطوبت می توانند بر خصوصیات مؤلفه تأثیر بگذارند و فرکانس برش واقعی را تغییر دهند.
کاربردهای عملی فیلترهای کم گذر
برای افزایش عملکرد و قابلیت اطمینان سیستم های الکترونیکی ، به ویژه در محیط هایی با تداخل و سر و صدا قابل توجه ، فیلترهای کم گذر مورد نیاز است.در منبع تغذیه دستگاه های الکترونیکی ، این فیلترها با از بین بردن نویز با فرکانس بالا ، ثبات و خلوص خروجی DC را تضمین می کنند.این سر و صدا می تواند از منابع مختلفی مانند اتصال خازنی و استقرایی از مدارهای اطراف سرچشمه بگیرد و می تواند عملکرد دستگاه را مختل کند.یک راه حل ساده و در عین حال مؤثر ، قرار دادن یک خازن در سراسر بار ، تشکیل یک فیلتر کم گذر است که اختلالات با فرکانس بالا را به دور از اجزای ناامن منحرف می کند.این روش به ویژه در تابلوهای مدار پر جمعیت ، که در آن تعداد زیادی از اجزای الکترونیکی در این نزدیکی هست ، مفید است و چالش هایی را برای حفظ یکپارچگی سیگنال ایجاد می کند.
انتخاب فیلتر - چه از خازن ها ، سلف ها و چه ترکیبی - به نیازهای خاص مدار ، از جمله نوع نویز و حساسیت اجزای پایین دست بستگی دارد.به عنوان مثال ، الکترونیک صوتی اغلب برای حفظ کیفیت سیگنال به طرح های فیلتر پیچیده ای نیاز دارد و از خروجی بی پروا اطمینان می یابد.فیلترهای کم گذر نه تنها برای کاهش نویز استفاده می شوند بلکه نقش مهمی در تبدیل آنالوگ به دیجیتال نیز دارند.آنها پهنای باند سیگنال ورودی را به فرکانس Nyquist محدود می کنند تا از بروز عواطف جلوگیری کنند ، که می تواند دقت تبدیل را کاهش دهد.در ارتباطات بی سیم ، این فیلترها سیگنال های با فرکانس بالا را در خارج از باند فرکانس مورد نظر مسدود می کنند و از تداخل و متقاطع بین کانال های ارتباطی جلوگیری می کنند.
فیلترهای کم گذر فراتر از مدارهای الکترونیکی سنتی مورد استفاده قرار می گیرند و بر زمینه های مختلف از رسانه های دیجیتال تا مراقبت های بهداشتی تأثیر می گذارد.
پالایش رسانه های بصری از طریق پردازش تصویر
در پردازش تصویر دیجیتال ، فیلترهای کم گذر با هموار سازی و تار شدن تصاویر ، کیفیت رسانه های تصویری را افزایش می دهند.این تکنیک باعث کاهش نویز پیکسل و مصنوعات با فرکانس بالا می شود که کیفیت تصویر را کاهش می دهد.این امر به ویژه در عکاسی دیجیتال و تولید فیلم ، که در آن تعادل وضوح تصویر با کاهش نویز تا حد زیادی بر جذابیت و وضوح بصری تأثیر می گذارد ، بسیار ارزشمند است.در برنامه های کاربردی در زمان واقعی مانند پخش ویدیو یا واقعیت افزوده ، فیلترهای کم گذر با وجود چالش های انتقال داده های زنده ، به حفظ کیفیت بصری بالا کمک می کنند.
اطمینان از وضوح در سیستم های ارتباطات
در ارتباطات از راه دور ، فیلترهای کم گذر با محدود کردن پهنای باند سیگنال های منتقل شده ، یکپارچگی سیگنال را برای جلوگیری از تداخل فرکانس بالا که می تواند داده ها را فاسد کند و ارتباط را مختل کند ، مدیریت می کنند.اطمینان از کیفیت سیگنال در مسافت های طولانی ، استفاده قابل توجهی در سیستم های ارتباطی آنالوگ و دیجیتال است.با استفاده از فیلترهای کم گذر ، خطاها کاهش می یابد و قابلیت اطمینان کلی کانال های ارتباطی افزایش می یابد.
افزایش دقت تشخیصی در کاربردهای زیست پزشکی
در زمینه زیست پزشکی ، فیلترهای کم گذر ، خوانایی و قابلیت اطمینان ضبط سیگنال فیزیولوژیکی مانند الکتروانسفالوگرام (EEG) و الکتروکاردیوگرام (ECG) را بهبود می بخشند.این دستگاه ها نسبت به سر و صدای با فرکانس بالا حساس هستند که می توانند داده های مهم را مبهم کنند و تشخیص دقیق را دشوار می کند.با ادغام فیلترهای کم گذر ، پزشکان پزشکی سیگنال های واضح تری ، بهبود روند تشخیص و تسهیل برنامه های درمانی مؤثرتر به دست می آورند.این برنامه اهمیت فیلتر در مراقبت های بهداشتی را برجسته می کند ، جایی که وضوح سیگنال های فیزیولوژیکی به طور مستقیم بر نتایج بیمار تأثیر می گذارد.
بهینه سازی سیستم های صوتی با فیلترهای کم گذر
فیلترهای کم گذر همچنین ابزاری همه کاره برای مهندسان صوتی هستند که به دستکاری در مناظر صوتی برای دستیابی به جلوه های مختلف هنری و فنی امکان می دهد.در اینجا روشهای ابتکاری این فیلترها در تنظیمات صوتی قابل استفاده است:
افزایش عمق مکانی در مخلوط ها
مهندسان صوتی از فیلترهای کم گذر برای اضافه کردن عمق و ابعاد به آهنگ های صوتی استفاده می کنند.با کاهش فرکانس های بالاتر ، می توان صداها را دورتر کرد.این اثر به ویژه در مخلوط های پیچیده مفید است که در آن تمایز بین عناصر پیش زمینه و پس زمینه باعث افزایش وضوح کلی و ادراک مکانی می شود.این تکنیک از تجربیات شنوایی در دنیای واقعی تقلید می کند ، جایی که فاصله به طور طبیعی فرکانس های بالاتر را فیلتر می کند ، و صداها را دورتر می کند.
تمیز کردن آهنگ های صوتی
در هر دو محیط صوتی استودیو و زنده ، فیلترهای کم گذر برای از بین بردن نویز با فرکانس بالا یا تداخل مفید هستند.موضوعات متداول مانند HISS ، HUM الکتریکی یا صداهای بیش از حد تیز از منابع دیجیتال می تواند به طور مؤثر به حداقل برسد.با قطع این فرکانس های ناخواسته ، صدای مورد نظر تمیزتر می شود ، وفاداری کلی تولید را بهبود می بخشد و یک محصول نهایی جلا را تضمین می کند.
فرکانس های متعادل در مخلوط های پیچیده
فیلترهای کم گذر برای مدیریت پوشش فرکانس مهم هستند ، یک چالش مشترک در تنظیمات موسیقی متراکم که در آن صداهای متعدد در همان محدوده فرکانس به رقابت می پردازند.مهندسان صوتی با ضعف انتخابی فرکانس های بالاتر در آهنگ های خاص ، می توانند از تحت الشعاع عناصر ضروری جلوگیری کنند ، یک محیط صوتی هماهنگ و متعادل را در ترکیب حفظ کنند.
ایجاد تغییرات صوتی
فیلترهای کم گذر به متخصصان صوتی اجازه می دهد تا تغییرات یک صدا را در یک ترکیب ایجاد کنند و چشم انداز شنوایی را غنی سازند.این امر می تواند به ویژه در افزودن تغییرات پویا در یک مسیر ، تغییر تایم و حضور صداها متناسب با بخش های مختلف یا تن های عاطفی مؤثر باشد ، در نتیجه روایت موسیقی را بدون معرفی عناصر جدید تقویت می کند.
پالایش تعریف صدا در مخلوط های متراکم
در مخلوط های صوتی پیچیده ، فیلترهای کم گذر ، تعریف و تمرکز صداهای خاص را تقویت می کنند.با کاهش فرکانس های بالاتر ، صدای باقیمانده واضح تر می شود و شنوندگان را قادر می سازد تا از جزئیات ظریف و ظرافت های در نظر گرفته شده بهتر قدردانی کنند.
بهینه سازی اتوبوس ها
فیلترهای کم گذر نیز در مدیریت اتوبوس های اثرات مانند Reverb یا تأخیر ارسال می شود.استفاده از این فیلترها فرکانسهای زیاد را کنترل می کند که در غیر این صورت ممکن است بر اثرات حاکم باشد ، و اطمینان حاصل می کند که آنها بدون اینکه مزاحم شوند ، به ترکیب اضافه می کنند.این کنترل دقیق ، تعادل کلی و زیبایی شناسی مخلوط را حفظ می کند و این امکان را می دهد تا به جای غلبه بر عناصر اصلی ، اثرات را تقویت کنند.
روشن کردن صداهای رقیب
مدیریت ماسک فرکانس ، که در آن صداهای متعدد برای همان فضای شنوایی رقابت می کنند ، یک چالش اختلاط رایج است.فیلترهای کم گذر در اینجا بسیار ارزشمند هستند ، زیرا آنها فرکانس های بالای برخی از آهنگ ها را کاهش می دهند تا از تحت الشعاع آنها جلوگیری کنند.این به حفظ یک ترکیب متعادل کمک می کند که در آن می توان از هر ساز یا آواز کاملاً قدردانی کرد.
کاوش در اشکال مختلف فیلترهای کم گذر
مدارهای فیلتر کم گذر در سیستم های مختلف الکترونیکی مهم هستند که به گونه ای طراحی شده اند که به سیگنال های با فرکانس پایین اجازه می دهند در حالی که فرکانس های بالاتر را کاهش می دهند ، عبور کنند.انتخاب نوع فیلتر بستگی به نیازهای خاص کاربردی و ویژگی های سیگنال مورد نظر دارد که هر نوع مزایای منحصر به فردی را ارائه می دهد.
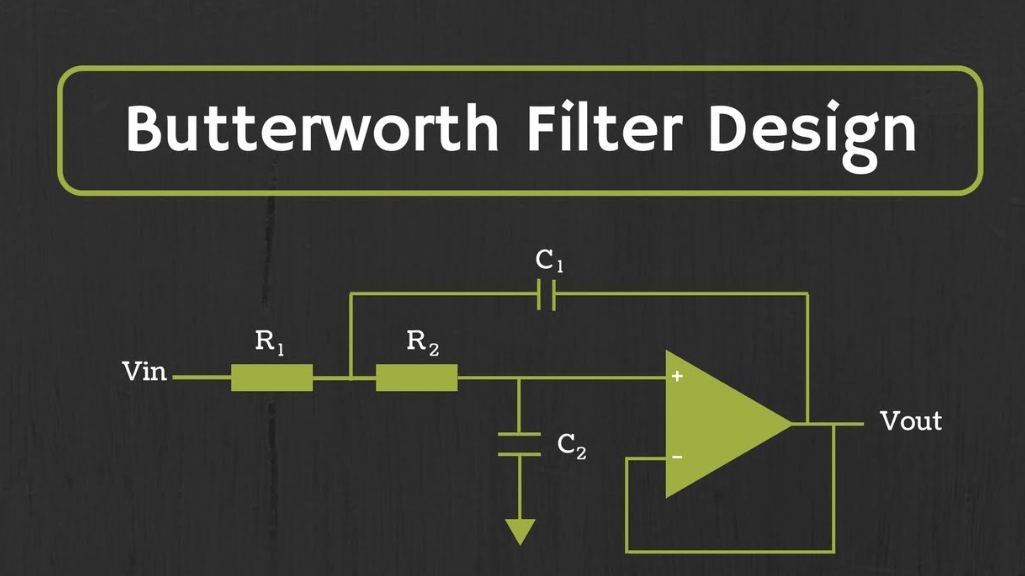
شکل 5: فیلترهای Butterworth
فیلترهای Butterworth به دلیل پاسخ پاس مسطح خود شناخته شده اند ، به این معنی که آنها هیچ گونه موج دار را در بند بند معرفی نمی کنند.این امر باعث می شود آنها برای پردازش صوتی و سایر برنامه های کاربردی ایده آل باشند که حفظ یکپارچگی سیگنال در داخل بند یک ضرورت است.طراحی آنها یک پاسخ خطی را تضمین می کند ، به حداقل رساندن اعوجاج سیگنال صوتی ، که برای سیستم های صوتی با وفاداری بالا و ابزارهای اندازه گیری دقیق قابل توجه است.
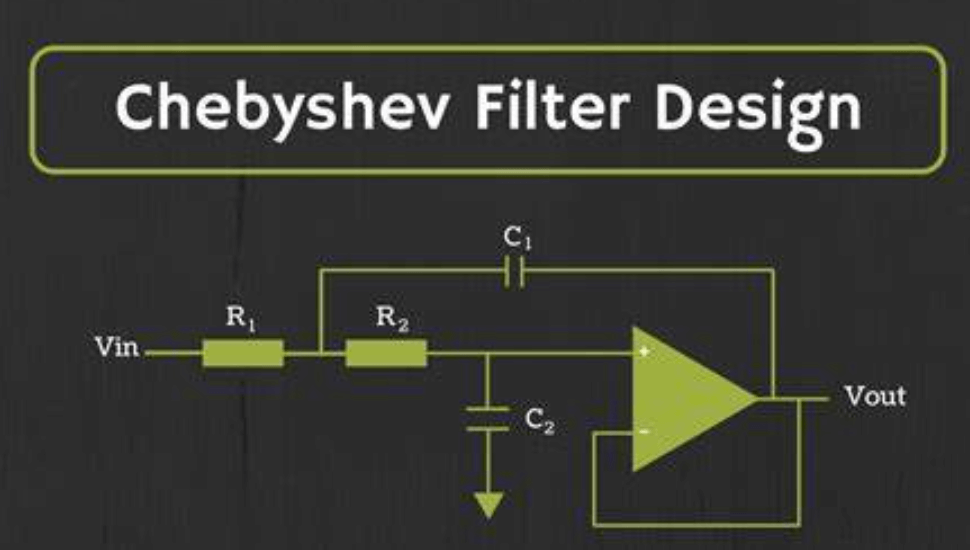
شکل 6: فیلترهای Chebyshev
فیلترهای Chebyshev از فیلترهای Butterworth به یک رول واضح تر دست می یابند و جدایی بهتری بین Passband و Stopband فراهم می کنند.این کار با هزینه برخی از ریپل ها در گذرگاه انجام می شود ، معامله ای قابل قبول در سناریوهایی که در آن یک برش شیب دار ناامن تر است.این فیلترها اغلب در سیستم های ارتباطی مورد استفاده قرار می گیرند ، جایی که محدودیت پهنای باند دقیق بیشتر از حداقل موج دارنده باند غالب است.
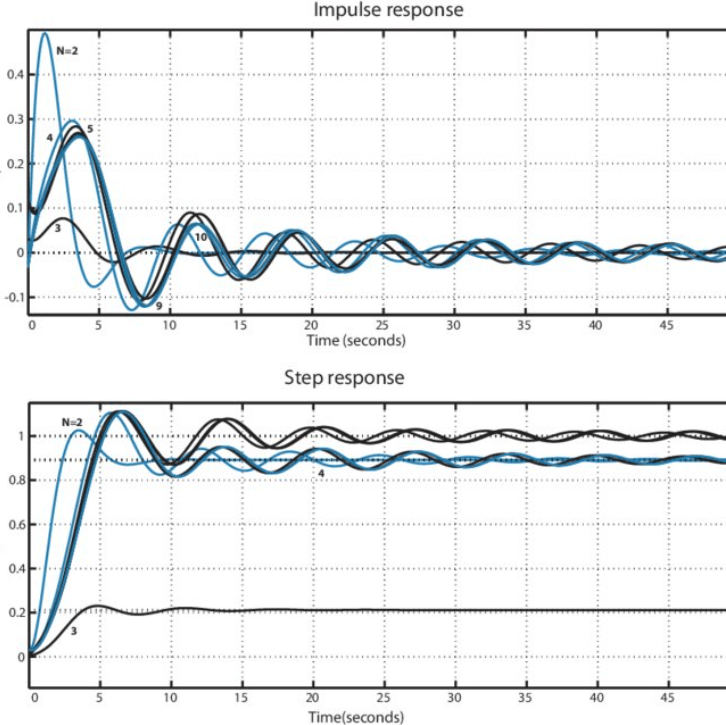
شکل 7: فیلترهای بیضوی
فیلترهای بیضوی (همچنین به عنوان فیلترهای Cauer نیز شناخته می شوند) شدیدترین حالت را ارائه می دهند و امکان انتقال حداقل از Passband به Stopband را فراهم می کنند.این امر باعث می شود آنها در برنامه هایی که تعداد فضا و مؤلفه ها محدود هستند ، مانند دستگاه های الکترونیکی قابل حمل و مینیاتوری ، موثر باشند.انتقال تیز در طیف های فرکانس متراکم بسته بندی شده مفید است ، جایی که به حداقل رساندن تداخل کانال مجاور قابل توجه است.
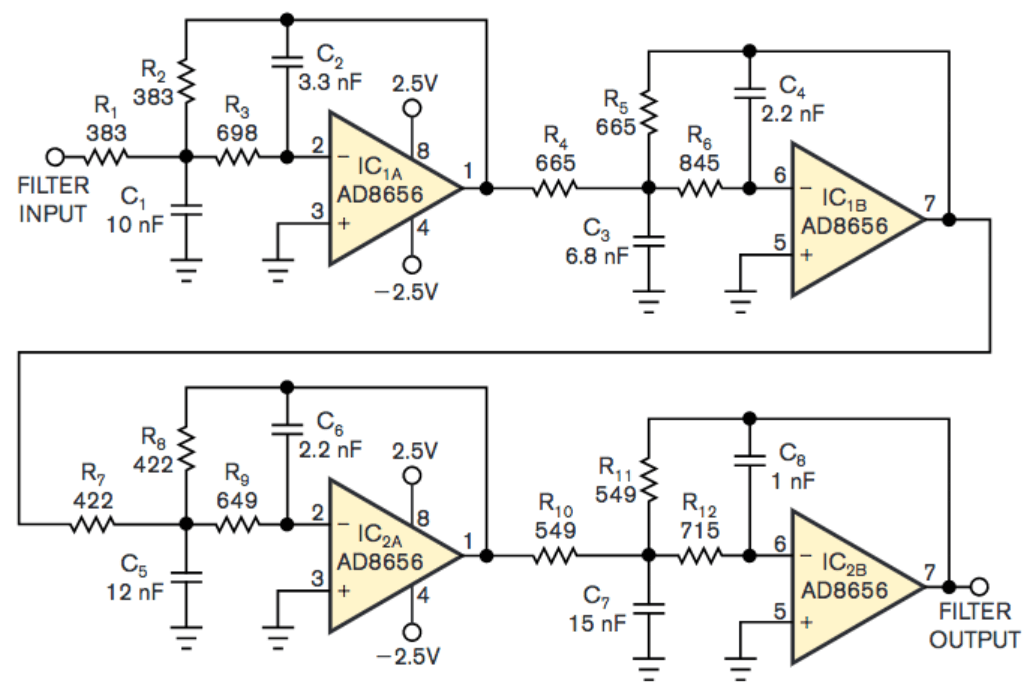
شکل 8: فیلترهای بسل
فیلترهای بسل ، ضمن ارائه یک راهپیمایی ملایم تر ، در حفظ فاز و شکل سیگنال ورودی در سراسر گذرگاه برتری دارند.این در برنامه هایی مانند ارتباطات پالس ، ابزار دقیق و متقاطع صوتی پویا است ، جایی که حفظ ویژگی های زمانی سیگنال اصلی ، دقت و وفاداری را تضمین می کند.
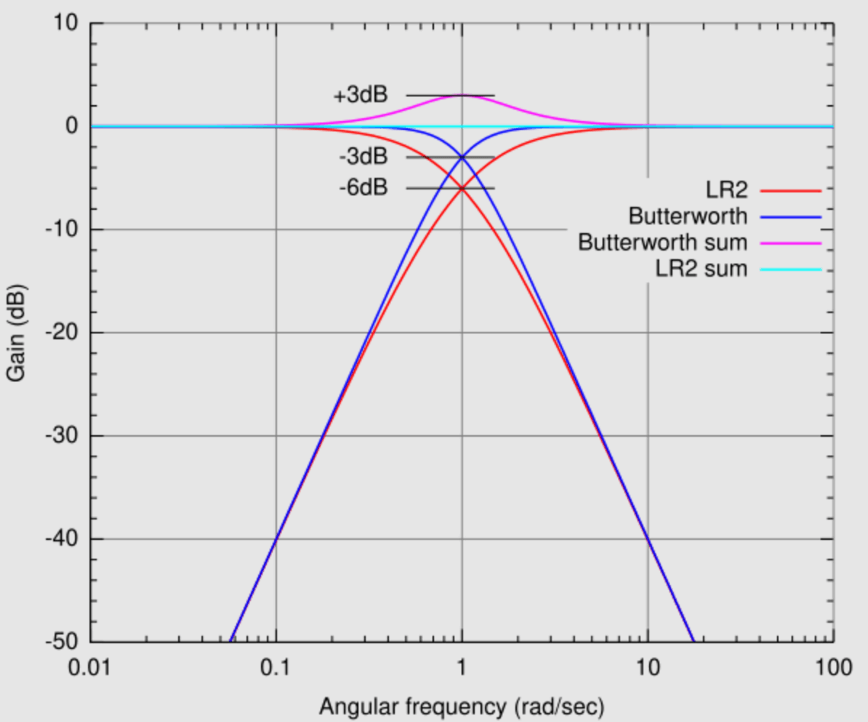
شکل 9: فیلتر Linkwitz-Riley
این فیلتر با شیب شیب دار 24 دسی بل/اکتاو ، کلید اصلی برنامه هایی است که تقسیم فرکانس دقیق مانند سیستم های بلندگو چند طرفه مورد نیاز است.در یک تنظیم بلندگو دو طرفه ، فیلتر LinkWitz-Riley فرکانس ها را دقیقاً تقسیم می کند و فرکانس های بالایی را به توییت و فرکانس های کم به ووفر می فرستد.این یک پاسخ فرکانس صاف با حداقل مسائل فاز را تضمین می کند ، که برای حفظ یکپارچگی صدا در محیط هایی که کیفیت صوتی ناامن است ، مانند استودیوهای ضبط حرفه ای یا سیستم های صوتی با وفاداری بالا پویا است.
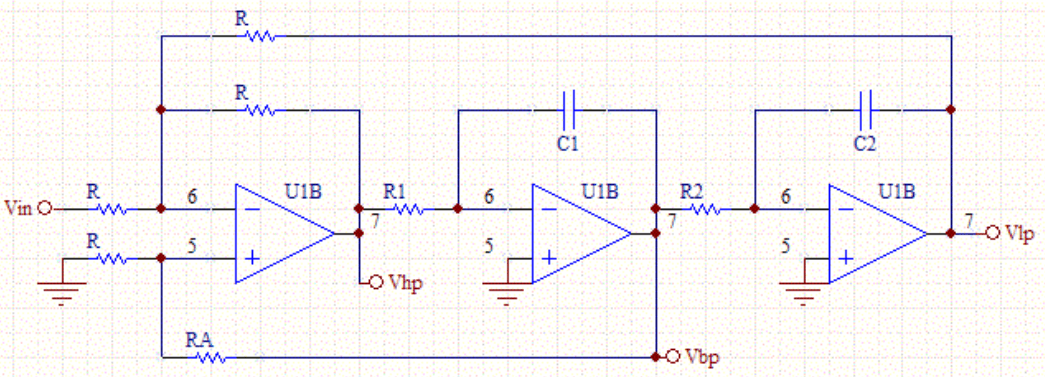
شکل 10: فیلتر متغیر حالت
فیلتر متغیر حالت به دلیل تطبیق پذیری و سودمندی در سنتز صدا قابل توجه است.بر خلاف فیلترهای سنتی ، خروجی های همزمان کم ، گذر بالا و گذر باند را ارائه می دهد.این عملکرد چند حالته امکان کنترل دقیق بر خصوصیات زمانی صدا در زمان واقعی را فراهم می کند و باعث می شود که برای ایجاد موسیقی الکترونیکی لازم باشد.توانایی انتقال هموار بین انواع فیلترهای مختلف به تولیدکنندگان کمک می کند تا بافت های صوتی پیچیده و تغییرات پویا در موسیقی خود را ایجاد کنند.در سینت سایزرها ، این فیلتر می تواند صداهایی را از باس های عمیق گرفته تا اوج های واضح تعدیل کند و این امر را برای طراحان صدا ضروری می کند.
شکل 11: فیلتر Moog
مشهور به دلیل صدای گرم ، غنی و کنترل رزونانس متمایز ، این ژانرهای مختلف موسیقی ، به ویژه موسیقی الکترونیکی را تحت تأثیر قرار داده است.فیلتر کم گذر MOOG صداهای سینت سایزر را افزایش می دهد ، از باس های عمیق تا سرب های صاف.ویژگی رزونانس آن فرکانس ها را در نقطه برش برجسته می کند و اوج ایجاد می کند که پیچیدگی هارمونیک را اضافه می کند.این امر باعث می شود که Moog فیلتر مورد علاقه در بین نوازندگان و تولید کنندگان باشد که به دنبال اضافه کردن عمق ، گرما و یک آنالوگ به آهنگ های خود هستند و میراث ماندگار آن در تولید موسیقی را تقویت می کنند.
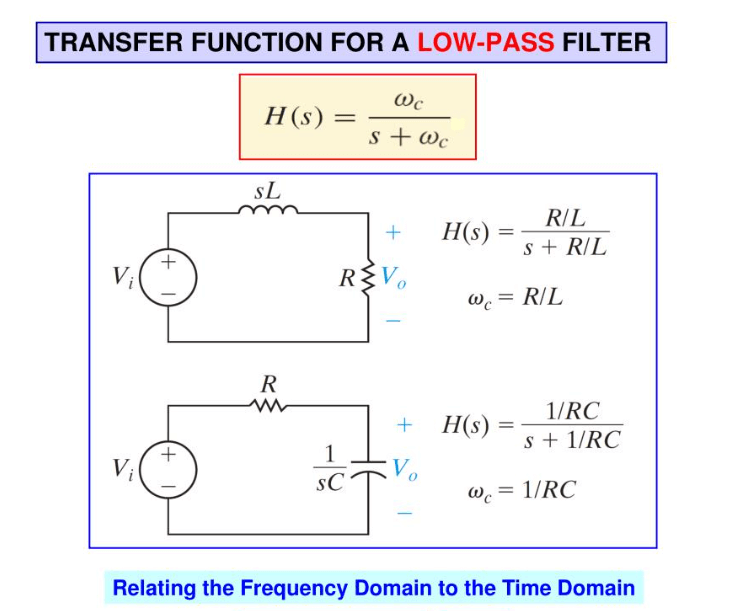
شکل 12: عملکرد انتقال در طراحی فیلتر کم گذر
تجزیه و تحلیل عملکرد انتقال فیلترهای کم گذر
ایجاد راه حل های کارآمد فیلتر نیاز به دانش گسترده ای از عملکرد انتقال فیلتر کم عبور دارد.این بیان ریاضی نشان می دهد که چگونه دامنه و فاز یک سیگنال خروجی نسبت به سیگنال ورودی در فرکانس های مختلف متفاوت است.عملکرد انتقال از اجزای فیلتر - مقاومت (R) ، خازن (C) و گاهی اوقات القاء (L) مشتق شده است و پاسخ فرکانس فیلتر را توصیف می کند.
عملکرد انتقال ، مشخص شده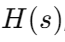 جایی که SSS متغیر فرکانس پیچیده است ، پویایی فیلتر را ضبط می کند.برای یک فیلتر کم گذر RC ساده ، عملکرد انتقال:
جایی که SSS متغیر فرکانس پیچیده است ، پویایی فیلتر را ضبط می کند.برای یک فیلتر کم گذر RC ساده ، عملکرد انتقال: 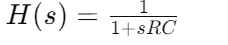 این معادله نشان می دهد که چگونه فیلتر سیگنال های فرکانس بالا را ضعیف می کند در حالی که اجازه می دهد فرکانس های کم با میرایی کمتر عبور کنند.محصول RC ، که به عنوان ثابت زمان شناخته می شود ، مستقیماً بر فرکانس برش تأثیر می گذارد ، نقطه ای که فیلتر شروع به کاهش چشمگیر فرکانس های بالاتر می کند.
این معادله نشان می دهد که چگونه فیلتر سیگنال های فرکانس بالا را ضعیف می کند در حالی که اجازه می دهد فرکانس های کم با میرایی کمتر عبور کنند.محصول RC ، که به عنوان ثابت زمان شناخته می شود ، مستقیماً بر فرکانس برش تأثیر می گذارد ، نقطه ای که فیلتر شروع به کاهش چشمگیر فرکانس های بالاتر می کند.
در پردازش صوتی ، عملکرد انتقال به سیستم هایی که کنترل فرکانس را برای حفظ کیفیت صدا و کاهش نویز کنترل می کنند ، کمک می کند.در ارتباطات از راه دور ، مهندسان را قادر می سازد مدارهایی را ایجاد کنند که سر و صدای با فرکانس بالا را فیلتر می کنند و از انتقال سیگنال واضح اطمینان می دهند.
عملکرد انتقال ابزاری خطرناک برای پیش بینی و تجزیه و تحلیل رفتار فیلتر در شرایط مختلف است.با تنظیم پارامترها در عملکرد انتقال ، طراحان می توانند ببینند که چگونه تغییرات در مقادیر مؤلفه بر عملکرد فیلتر تأثیر می گذارد.این امر به ویژه در فرآیندهای طراحی تکراری مفید است ، جایی که برای دستیابی به نتایج بهینه ، نمونه های اولیه ممکن است آزمایش شوند.
تسلط بر کنترل فیلترهای کم گذر
فیلترهای کم گذر نقش اصلی را در شکل دادن به سیگنال های صوتی ایفا می کنند و امکان کنترل دقیق بر روی کدام فرکانس ها را برجسته یا کاهش می دهند.در این بخش به بررسی اصول و کارکردهای اصلی فیلترهای کم گذر ، تأکید بر نقش مورد نیاز آنها در پردازش صوتی می پردازیم.
شیب و رزونانس
شیب یک فیلتر کم گذر نشان می دهد که فرکانس های بالاتر از برش به سرعت کاهش می یابد و بر خروجی فیلتر تأثیر می گذارد.شیب تندتر به معنای افت واضح تر در فرکانس های زیاد است و به منزوی کردن فرکانس های پایین تر به طور مؤثر کمک می کند.علاوه بر این ، کنترل رزونانس می تواند فرکانس ها را در برش تقویت کند ، و یک کیفیت صدا منحصر به فرد را اضافه می کند و باعث افزایش تن های خاص می شود.این کنترل به تولید کنندگان اجازه می دهد تا نشاط را اضافه کنند و شخصیت موسیقی را تعریف کنند.
عامل q
عامل Q یا فاکتور کیفیت ، پهنای باند را در مورد فرکانس برش که در آن رزونانس قابل توجه است ، اندازه گیری می کند.یک عامل Q بالا بر طیف وسیعی از فرکانس ها تأکید می کند و تمرکز بیشتری را به آن منطقه می بخشد.یک فاکتور Q کم رزونانس را در محدوده وسیع تری گسترش می دهد و پاسخ فرکانس را هموار می کند.این پارامتر کانونی برای مهندسان صوتی است که با هدف شخصی سازی صداها برای تأمین نیازهای خاص هنری یا فنی انجام می شود.
مدولاسیون از طریق پیروان پاکت
کنترل های مدولاسیون ، مانند یک پیروان پاکت ، پاسخ پویا فیلترهای کم گذر را با تغییر فرکانس برش در زمان واقعی با توجه به دامنه سیگنال ورودی تقویت می کنند.این ویژگی به فیلتر اجازه می دهد تا با پویایی قطعه موسیقی سازگار شود و پیچیدگی ریتمیک و بافتی را اضافه کند.کنترل مدولاسیون خارجی امکانات خلاقانه در طراحی صدا را گسترش می دهد ، و آن را در موسیقی الکترونیکی به ویژه ارزشمند می کند ، جایی که تغییرات بافتی پویا می تواند به طور قابل توجهی بر احساس و پیشرفت آهنگ تأثیر بگذارد
پایان
اکتشاف فیلترهای کم گذر در دامنه های مختلف ، نقش ضروری آنها را در فناوری معاصر تأکید می کند.از پالایش مخلوط های صوتی در تولید موسیقی گرفته تا افزایش قابلیت اطمینان سیستم های ارتباطی الکترونیکی ، فیلترهای کم گذر با طیف متنوعی از چالش ها سازگار می شوند و از عملکرد بهینه و وفاداری اطمینان می دهند.بررسی دقیق انواع مختلف فیلتر ، مانند فیلترهای Butterworth ، Chebyshev و Moog ، مزایای منحصر به فرد آنها را در برنامه های خاص نشان می دهد و ضرورت طراحی فیلتر متناسب را برای برآورده کردن خواسته های عملیاتی دقیق نشان می دهد.
ادغام ابزارهای شبیه سازی پیشرفته و در نظر گرفتن عمیق پویایی فرکانس برش ، توانایی پیش بینی و رفتار فیلتر دقیق را در شرایط دنیای واقعی تقویت می کند.با پیشرفت فناوری ، تکامل مداوم طرح های فیلتر کم گذر ، بدون شک نقش مهمی در پیشرفت مهندسی الکترونیکی و تولید صدا دارد و حک شده ای برای راه حل های نوآورانه که هم چالش های فعلی و هم آینده را در پردازش سیگنال می گیرند.
سوالات متداول [سؤالات متداول]
1. فیلتر پر گذر و کم عبور چیست؟
یک فیلتر با گذر بالا اجازه می دهد تا فرکانس های بالاتر از یک فرکانس برش خاص عبور کند و فرکانس های زیر این برش را ضعیف کند.برعکس ، یک فیلتر کم گذر اجازه می دهد تا فرکانس های زیر یک فرکانس برش خاص عبور کند و از بالای آن ضعیف شود.
2. مزایای فیلتر کم گذر چیست؟
کاهش نویز: آنها به طور موثری نویز با فرکانس بالا را کاهش می دهند و باعث می شوند آنها در پردازش سیگنال صوتی و الکترونیکی مفید باشند.
هموار سازی سیگنال: از فیلترهای کم گذر برای صاف کردن داده ها با میانگین نوسانات سریع ، مفید در تجزیه و تحلیل داده ها و برنامه های مدار الکترونیکی استفاده می شود.
پایداری: آنها با فیلتر کردن نوسانات با فرکانس بالا در تثبیت سیستم های کنترل کمک می کنند.
3. هدف از فیلترهای کم گذر در پردازش تصویر چیست؟
در پردازش تصویر ، یک فیلتر کم گذر برای تار شدن تصاویر ، که می تواند باعث کاهش نویز و جزئیات شود ، خدمت می کند.این اثر تار باعث تغییر سریع شدت می شود ، که به تقویت و تجزیه و تحلیل تصویر کمک می کند ، به ویژه در از بین بردن جزئیات در مقیاس کوچک برای تمرکز بر ساختارهای بزرگتر.
4- فیلترهای کم عبور فعال چگونه کار می کنند؟
فیلترهای کم گذر فعال از اجزای فعال مانند تقویت کننده ها ، همراه با مقاومت و خازن ، برای فیلتر کردن سیگنال ها استفاده می کنند.آمپلی فایر از دست دادن سیگنال به دلیل فیلتر جبران می کند ، بنابراین قدرت سیگنال را حفظ می کند.این تنظیم به فیلتر اجازه می دهد تا سیگنال های با فرکانس پایین را به طور مؤثر و بدون تخریب قابل توجهی اداره کند و به دلیل ماهیت فعال آن به راحتی در مدارهای الکترونیکی مختلف ادغام شود.
5- مضرات فیلتر کم گذر چیست؟
از دست دادن جزئیات قابل توجه: با ضعف فرکانس های بالا ، برخی از جزئیات مهم در سیگنال ها ، مانند انتقال تیز یا ویژگی های سیگنال خاص ، ممکن است از بین برود.
تغییر فاز: آنها می توانند تغییر فاز در سیگنال های فیلتر شده را معرفی کنند ، که ممکن است در برنامه های کاربردی که نیاز به تراز دقیق فاز دارند ، مشکل ساز باشد.
پیچیدگی طراحی: طراحی یک فیلتر کم گذر مؤثر که به طور دقیق فرکانس برش و یکپارچگی سیگنال را متعادل می کند ، می تواند پیچیده باشد ، به خصوص در فیلترهای فعال که در آن انتخاب مؤلفه و عملکرد تأثیر.
دربارهی ما
ALLELCO LIMITED
ادامه مطلب
پرس و جو سریع
لطفاً یک سؤال ارسال کنید ، ما بلافاصله پاسخ خواهیم داد.
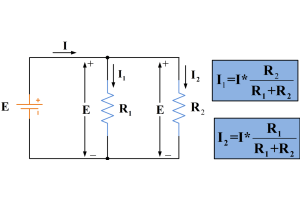
مدارهای تقسیم کننده فعلی و استفاده مؤثر از فرمول تقسیم کننده
در 2024/06/14
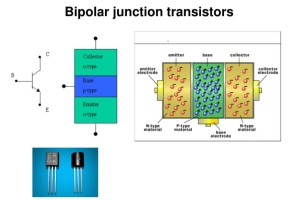
یک راهنمای کامل برای درک ترانزیستورهای اتصال دو قطبی (BJT)
در 2024/06/13
پست های محبوب
-
GND در مدار چیست؟
در 1970/01/1 2941
-

راهنمای اتصال RJ-45: کدهای رنگی اتصال RJ-45 ، طرح های سیم کشی ، برنامه های R-J45 ، برگه های داده RJ-45
در 1970/01/1 2501
-

انواع اتصال فیبر: SC در مقابل LC و LC در مقابل MTP
در 1970/01/1 2089
-
ولتاژ منبع تغذیه در الکترونیک VCC ، VDD ، VEE ، VSS و GND
در 0400/11/9 1895
-

مقایسه بین DB9 و Rs232
در 1970/01/1 1765
-

باتری LR44 چیست؟
برق ، آن نیروی همه گیر ، بی سر و صدا همه جنبه های زندگی روزمره ما را نفوذ می کند ، از وسایل بی اهمیت گرفته تا تجهیزات پزشکی تهدید کننده زندگی ، این نقش خاموش را ایفا می کند.با این حال ، درک این انرژی ، به ویژه نحوه ذخیره و کارآ...در 1970/01/1 1714
-

درک اصول: مقاومت در برابر القاء ، و مقادیر
در رقص پیچیده مهندسی برق ، سه گانه از عناصر اساسی مرحله مرکزی را به خود اختصاص می دهد: القاء ، مقاومت و ظرفیت.هر یک از صفات منحصر به فرد را نشان می دهد که ریتم پویا مدارهای الکترونیکی را دیکته می کند.در اینجا ، ما به سفری برا...در 1970/01/1 1655
-

راهنمای جامع باتری CR2430: مشخصات ، برنامه ها و مقایسه با باتری های CR2032
باتری CR2430 چیست؟مزایای باتری CR2430هنجاربرنامه های باتری CR2430معادل CR2430CR2430 در مقابل CR2032اندازه باتری CR2430هنگام خرید CR2430 و معادل ها به دنبال چه چیزی باشیدبرگه داده PDFسوالات متداول باتری ها قلب دستگاه های الکترونیکی کوچک هستند.د...در 1970/01/1 1555
-
RF چیست و چرا از آن استفاده می کنیم؟
فناوری فرکانس رادیویی (RF) بخش مهمی از ارتباطات بی سیم مدرن است و امکان انتقال داده ها در مسافت های طولانی و بدون اتصالات فیزیکی را فراهم می کند.این مقاله به اصول اولیه RF می پردازد و توضیح می دهد که چگونه تابش الکترومغناطیسی...در 1970/01/1 1541
-

CR2450 در مقابل CR2032: آیا می توان از باتری به جای آن استفاده کرد؟
باتری های منگنز لیتیوم با سایر باتری های لیتیوم شباهت دارند.چگالی انرژی بالا و عمر طولانی مدت ویژگی هایی است که آنها مشترک هستند.این نوع باتری به دلیل ایمنی منحصر به فرد ، اعتماد و نفع بسیاری از مصرف کنندگان را به دست آورد...در 1970/01/1 1512
















































