خانه وبلاگ~~راهنمای دقیق برای تبلیغ کامل~~

~~در 2024/05/10~~ ~~603~~

راهنمای دقیق برای تبلیغ کامل

در حوزه الکترونیک دیجیتال و مهندسی رایانه ، افزودنی ها یکی از مهمترین بلوک های ساختمانی ، محوری در ساخت و عملکرد مدارهای حسابی پیچیده تر را نشان می دهند.به عنوان مؤلفه های جدایی ناپذیر واحد منطق حسابی (ALU) ، افزودنی ها عملیات محاسباتی بی شماری را تسهیل می کنند ، از حسابی اساسی گرفته تا کارهای منطقی پیچیده لازم برای عملکرد سیستم.طراحی آنها ، که می تواند از نیمه های ساده و ساده تا افزودنی های پیچیده تر متفاوت باشد ، نقش مهمی در افزایش کارآیی و سرعت پردازش در سیستم های دیجیتال دارد.این مقاله به معماری دقیق و تفاوت های عملکردی انواع مختلف افزودنی ها می پردازد و نقش مهم آنها را در فناوری محاسبات مدرن نشان می دهد و منطق عملیاتی ، مدار و برنامه های کاربردی آنها را در زمینه گسترده تر طراحی منطق دیجیتال نشان می دهد.

کاتالوگ

1. ADDER چیست؟

2. نیمی از تبلیغ

3. تبلیغ کامل

4- جدول حقیقت تبلیغی کامل

5- مشخصات معادلات یک تبلیغ کامل

6. اجرای یک مدار کامل ADDER

7. مزایا و مضرات افزودنی کامل

8. برنامه های کاربردی کامل در منطق دیجیتال

9. نمونه هایی از اجرای کامل Adder

10. نتیجه گیری

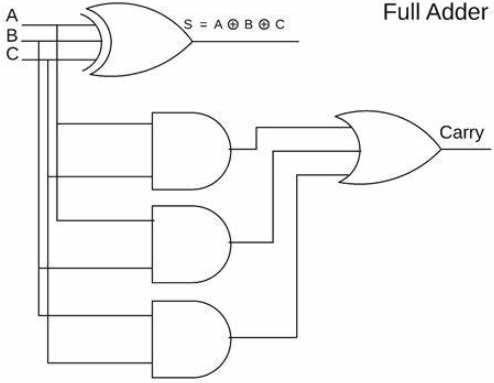
شکل 1: تبلیغ کامل

adder چیست؟

یک ADDER یک مؤلفه اساسی در مهندسی الکترونیکی و طراحی منطق دیجیتال است و در سیستم های رایانه ای پیچیده تر نقش اصلی را ایفا می کند.به عنوان بخشی از واحد منطق حسابی (ALU) ، Adder انواع کارهای محاسباتی اساسی را انجام می دهد.کارآیی و عملکرد کل پردازنده به طور مستقیم تحت تأثیر طراحی و عملکرد ADDER قرار می گیرد.

در پردازنده ، ADDER نه تنها برای عملیات اساسی حسابی مانند افزودن و تفریق استفاده می شود ، بلکه در طیف گسترده تری از عملیات منطقی نیز درگیر می شود.به عنوان مثال ، هنگام اجرای برنامه ها ، پردازنده اغلب نیاز به محاسبه آدرس های حافظه جدید دارد.این کار به طور معمول با اضافه کردن یا کم کردن از آدرس فعلی انجام می شود - وظیفه ای که توسط Adder انجام می شود.آنها تعداد تکرارهای حلقه و جریان کلی را با افزایش و کاهش پیشخوان کنترل می کنند.در برنامه های پیچیده تر ، مانند نمایه سازی جدول ، افزودنی ها به سرعت داده ها را با محاسبه جبران خسارت پیدا می کنند.این برای سیستم های مدیریت پایگاه داده ، ساخت کامپایلر و پردازش داده های در مقیاس بزرگ مهم است.افزودنی ها همچنین در اجرای برخی از تکنیک های نقشه برداری در سیستم های حافظه نهان چند سطحی ، با استفاده از عملیات حسابی برای تعیین موقعیت داده ها در حافظه نهان ، مهم هستند ، بنابراین بهینه سازی راندمان دسترسی.

از نظر فنی ، افزودنی ها از طریق طرح های مختلف مدار از جمله افزودنی های موازی ، سریال و خط لوله اجرا می شوند.افزودنی های موازی به دلیل توانایی خود در رسیدگی به چندین رقم به طور همزمان مورد حمایت قرار می گیرند ، و آنها را برای سناریوهایی که نیاز به محاسبات سریع دارند ، مناسب می کند.از طرف دیگر ، افزودنی های سریال ، یک بیت را در هر چرخه ساعت پردازش می کنند و برای محیط های محدود یا کم مصرف منابع ایده آل هستند.افزودنی های خط لوله روند اضافی را به چندین مرحله تقسیم می کنند که هر یک بخشی از عملیات اضافی را اداره می کنند.این طرح به طور قابل توجهی سرعت محاسبه را افزایش می دهد ، به خصوص در محیط های محاسباتی با کارایی بالا.

نصف تبلیغ

یک مدار نیمه آدرس یک ساختمان اساسی در الکترونیک دیجیتال است ، که به طور خاص برای اضافه کردن دو رقم باینری منفرد طراحی شده است.این مدار پایه و اساس یک تبلیغ کامل را تشکیل می دهد و برای درک طرح های پیچیده تر مدار منطقی مهم است.در نیمی از تبلیغات ، دو ورودی اصلی وجود دارد که دارای برچسب A و B هستند که به ترتیب اضافه و افزودنی را نشان می دهند.این تنظیم آن را قادر می سازد بدون نیاز به ورودی حمل از محاسبات قبلی ، مبلغ را محاسبه و خروجی انجام دهد.

هسته اصلی یک افزودنی از دو دروازه منطقی تشکیل شده است: یک دروازه Xor و An و Gate.دروازه XOR وظیفه تولید خروجی جمع را بر عهده دارد.این قانون تحت یک قانون ساده عمل می کند که در صورتی که فقط یکی از ورودی های آن 1 باشد ، 1 را صادر می کند.در غیر این صورت ، از طرف دیگر دروازه و دروازه را به دست می آورد.این 1 تنها در شرایطی که هر دو ورودی آن 1 باشد ، تولید می کند و کاملاً با نیازهای اساسی افزودن باینری هماهنگ است.

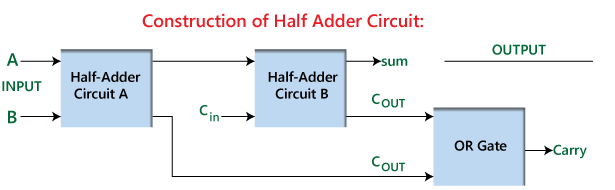
شکل 2: ساخت نیمی از تبلیغات

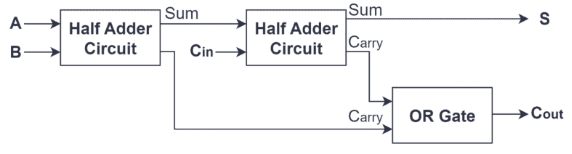
این طراحی کارآمد و ساده به نیمی از Adder اجازه می دهد تا نه تنها اضافه کردن باینری اساسی را به طور مستقل انجام دهد بلکه به عنوان یک ساختمان ساختمانی برای ایجاد یک تبلیغ کامل نیز خدمت می کند.یک تبلیغ کامل با ترکیب دو نیمی از افزودنی ها با یک دروازه اضافی یا دروازه ساخته شده است.در این تنظیم ، نیمه اول Adder کار اضافه اولیه را انجام می دهد و مبلغ اولیه و حمل را نیز تولید می کند.نیمه دوم Adder سپس حمل را از اول به همراه ورودی حمل اضافی پردازش می کند.سرانجام ، دروازه OR دو خروجی حمل را برای تولید خروجی نهایی انجام می دهد.این ترتیب عملکرد ADDER را تقویت می کند ، و این امکان را برای انجام کارهای پیچیده تر چند بیتی پیچیده تر ، نمایش کاربرد گسترده و اهمیت نیمی از افزودنی ها در طراحی مدار دیجیتال فراهم می کند.

تبلیغ کننده کامل

یک adder کامل یک مؤلفه پیشرفته در طراحی منطق دیجیتال است ، مجهز به افزودن سه ورودی باینری تک بیتی است که معمولاً به عنوان A ، B و حمل (CIN) برچسب گذاری می شود.این طرح به ADDER کامل اجازه می دهد تا با وارد کردن CART از محاسبات قبلی مرتبه پایین در یک عملیات واحد ، افزودنی های باینری پیچیده را به طور مؤثر پردازش کند.

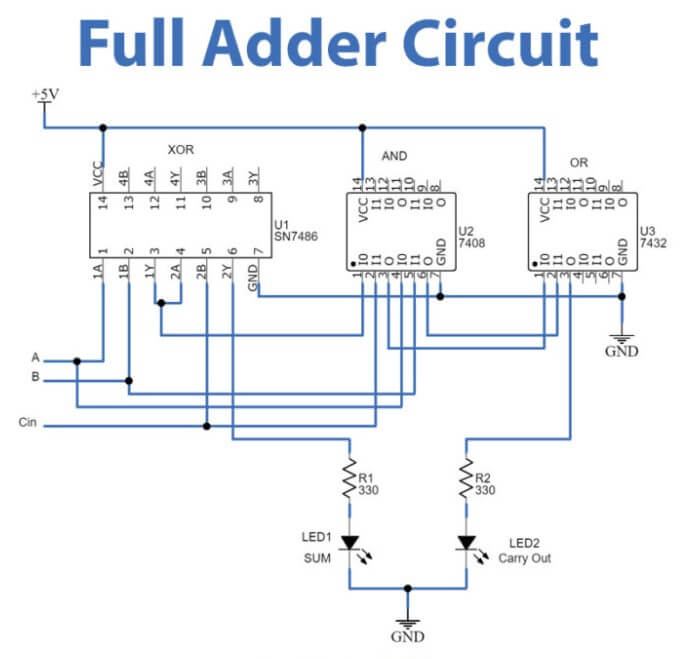
شکل 3: مدار تبلیغاتی کامل

از نظر عملکردی ، یک Adder کامل می تواند یک مبلغ دو رقمی را تولید کند ، به این معنی که خروجی آن می تواند از 0 تا 3 باشد و همچنین می تواند یک حمل و نقل (COUT) را نیز تولید کند.این اتفاق می افتد زیرا ، هنگامی که تمام بیت های ورودی روی 1 تنظیم می شوند (A = 1 ، B = 1 ، CIN = 1) ، خروجی مبلغ 1 خواهد بود (نشان دهنده باینری 01) ، و حمل 1 تولید می شود ، نشان می دهد که این نشان می دهدحمل اضافی باید به بیت بالاتر بعدی منتقل شود.

از نظر ساختاری ، Adder کامل به طور کلی از دو نیمی از اضافه کننده و یک یا دروازه تشکیل شده است.نیمی از Adder ورودی های A و B را می گیرد و مبلغ اولیه و سیگنال حمل را تولید می کند.این مبلغ اولیه سپس به همراه حمل (CIN) به نیمه دوم اضافه می شود.نقش نیمه دوم Adder اضافه کردن این مبلغ از نیمه اول Adder به CIN ، تولید مبلغ دیگری و یک خروجی جدید است.به طور همزمان ، خروجی حمل از نیمه اول و خروجی حمل از نیمه دوم Adder از طریق یک دروازه OR ادغام می شود و در نتیجه نهایی (COUT) از Adder کامل به اوج خود می رسد.طراحی این ساختار تضمین می کند که Adder کامل به طور موثری انتشار حامل ها را علاوه بر عملیات انجام می دهد ، و آن را برای اجرای اضافات باینری چند بیتی ایده آل می کند.بنابراین ، طراحی Adder کامل نه تنها پردازش داده ها را سرعت می بخشد و کارآیی را تقویت می کند بلکه پیچیدگی اجرای سخت افزار را از طریق ترکیبی ساده از دروازه های منطقی ساده می کند ، و آن را به یک مؤلفه ضروری در افزودن چند رقمی و واحد منطق حسابی تبدیل می کند (ALU).

پارامترها	نصف تبلیغ	تبلیغ کننده کامل
شرح	نیمی از Adder یک منطق ترکیبی است مدار که دو رقم 1 بیتی اضافه می کند.نیمه آدرس مبلغی از این دو را تولید می کند ورودی ها	یک تبلیغ کامل یک منطق ترکیبی است مدار که عملکرد اضافی را روی سه عدد باینری یک بیتی انجام می دهد. Adder کامل مبلغی از سه ورودی و ارزش حمل را تولید می کند.
حمل قبلی	از حمل قبلی استفاده نمی شود.	از حمل قبلی استفاده می شود.
ورودی	در نصف تبلیغ ، دو بیت ورودی وجود دارد (الف ، ب).	در تبلیغ کامل ، سه بیت ورودی وجود دارد (A ، B ، C_در).
بازده	خروجی تولید شده از دو بیت است و از ورودی 2 بیت حمل کنید.	خروجی تولید شده از دو بیت است و از ورودی 3 بیت حمل کنید.
به عنوان	از یک مدار نیمه آدرید نمی توان در آن استفاده کرد به همان روشی که یک مدار کامل است.	از یک مدار کامل تبلیغی می توان در محل استفاده کرد از یک مدار نیمی از Adder.
نشان	اجرای آن ساده و آسان است	طراحی یک تبلیغ کامل به این صورت نیست ساده به عنوان یک نیمی از تبلیغات.
بیان منطقی	بیان منطقی برای نیمی از adder: s = a⊕b ؛c = a*b.	بیان منطقی برای تبلیغ کامل: s = a⊕b⊕cin ؛جف_خارج= (ab)+(c_در(a⊕b)).
دروازه های منطقی	این شامل یک دروازه سابق یا یک و یک و دروازه	این شامل دو دو ، دو و دروازه است ، و یک یا دروازه
برنامه	در ماشین حساب ها ، رایانه ها ، دستگاه های اندازه گیری دیجیتال و غیره	از آن در موارد اضافی بیت استفاده می شود ، پردازنده های دیجیتال و غیره
نام جایگزین	هیچ نام متفاوتی برای نیمی وجود ندارد تبلیغ	یک تبلیغ کامل نیز به عنوان یک حمل و نقل موج دار شناخته می شود تبلیغ

نمودار 1: تفاوت بین نیمی از تبلیغات و تبلیغ کامل

جدول حقیقت تبلیغ کامل

جدول حقیقت یک تبلیغ کامل ، کلید درک منطق عملیاتی آن است و جزئیات رابطه دقیق بین ترکیبات ورودی باینری و خروجی های مربوطه آنها را شرح می دهد.این جدول تمام سناریوهای ورودی بالقوه و نتایج آنها را نشان می دهد و آن را به ابزاری اساسی در طراحی و تأیید مدارهای منطق دیجیتال تبدیل می کند.ADDER کامل سه ورودی را پردازش می کند: A ، B و یک حمل (CIN) که هر یک از آنها می تواند 0 یا 1 باشد. این منجر به هشت ترکیب احتمالی ورودی می شود.

برای هر یک از این ترکیبات ، خروجی های موجود از ADDER شامل یک مبلغ (مبلغ) و حمل (COUT) است.مبلغ افزودنی Modulo-2 (عملیات XOR) از سه ورودی-A ، B و CIN است.حمل و نقل هنگامی اتفاق می افتد که حداقل دو مورد از بیت های ورودی 1 باشد. این نشان دهنده توانایی کامل Adder برای رسیدگی به حمل و نقل در عملیات افزودنی متوالی ، و اطمینان از صحت در محاسبات بیت بالاتر است.

برای نشان دادن ، سناریوی ورودی را در نظر بگیرید که تمام ورودی ها 0 هستند (A = 0 ، B = 0 ، C-in = 0).مبلغ خروجی 0 خواهد بود و حمل نیز 0 خواهد بود ، نشان می دهد که هیچ مبلغ اضافی یا حمل برای مدیریت وجود ندارد.اگر فقط یک بیت ورودی 1 باشد ، مانند A = 1 ، b = 0 ، c-in = 0 ، مبلغ خروجی 1 بدون حمل خواهد بود ، نشان می دهد که نیازی به انتقال حمل به بیت بالاتر نیست.هنگامی که دو بیت ورودی 1 است ، مانند A = 1 ، B = 1 ، C-in = 0 ، مبلغ خروجی 0 است (از آنجاخارج از 1 است ، نشانگر حمل است که باید به بیت بالاتر بعدی منتقل شود.پیچیده ترین سناریو هنگامی اتفاق می افتد که هر سه بیت ورودی 1 باشد (A = 1 ، B = 1 ، C-in = 1).مبلغ خروجی 1 است و از 1 استفاده می شود ، نشان می دهد که مدیریت حمل نیز ممکن است در بیت های بالاتر نیز لازم باشد.

بوها	بشور	جف_در	حرف	جف_خارج
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

نمودار 2: جدول حقیقت تبلیغی کامل

مشخصات معادلات یک تبلیغ کامل

درک کامل ADDER شامل جدا کردن عملکرد آن با استفاده از جدول حقیقت است ، جایی که ترکیب های مختلف مقادیر ورودی A ، B و C-in منجر به خروجی و COUT می شوند.برای درک عملکرد ، معادلات منطقی را به صورت مرحله به مرحله ساده می کنیم.

بیان منطقی برای جمع

معادله با موارد متمایز شروع می شود که مبلغ آن برابر است 1:

• a 'b' cin + a 'b cin' + a b 'cin' + ab cin

این معادله را می توان با گروه بندی شرایط با و بدون CIN متراکم کرد:

• CIN (A 'B' + AB) + CIN '(A' B + A B ')

این ساده سازی منجر به یک فرم آسان برای اجرای می شود:

• CIN XOR (A Xor B)

این بازنمایی نشان می دهد که خروجی جمع در اصل عملکرد XOR در بین A ، B و CIN است ، و رفتار اصلی افزودن باینری را ضبط می کند که در آن جمع بر اساس تعداد عجیب و غریب است.

منطق برای cout

شروع با شرایطی که حمل تولید می شود:

• a 'b cin + a b' cin + ab c-in ' + ab cin

ساده سازی معادله ، ما اصطلاحاتی را که معمولاً شامل تولید حمل هستند ، شناسایی می کنیم:

• AB + B CIN + A CIN

به دنبال روش دیگری برای اجرای COUT ، معادله می تواند دوباره سازماندهی شود:

• ab + a cin + b c-in (a + a ')

این گسترش می یابد و نوترکیب ها برای ضبط تمام سناریوهایی که حداقل دو ورودی 1 است:

• AB CIN + AB + A C-in + A 'B CIN

• AB (1 + CIN) + A C-in + A 'B CIN

• ab + a c-in (b + b ') + a' b cin

• AB + A B 'CIN + A' B CIN

• ab + cin (a 'b + a b')

فرم جمع و جور نهایی برای Cout:

• ab + cin (a xor b)

این نسخه از معادله حمل و نقل نشان می دهد که چگونه COUT یا هنگامی که هر دو A و B 1 هستند ، یا هنگامی که یکی از A یا B 1 به همراه حمل و نقل است ، تولید می شود ، بنابراین منطق مورد نیاز برای مدیریت انتشار در چنداضافه کردن باینری کمی.این منطق ساده به ویژه برای اجرای مدارهای دیجیتال کارآمد مفید است.

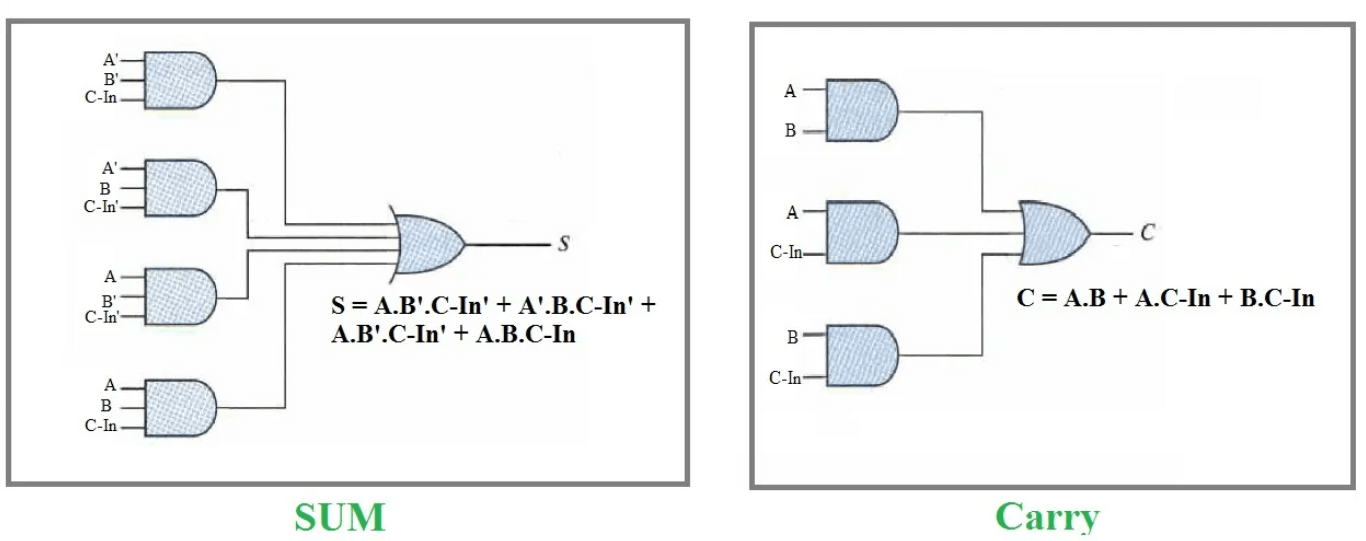
شکل 4: معادلات یک تبلیغ کامل

اجرای یک مدار کامل Adder

اجرای یک مدار کامل ADDER شامل مونتاژ دقیق دو نیمی از اضافه کننده و یک دروازه برای ایجاد دستگاهی است که قادر به دستیابی به کارآمد افزودن سه ورودی باینری تک بیتی است.این ترتیب پیچیدگی مدار را بهینه می کند و هم محاسبات کارآمد و دقیق را تضمین می کند.

برای شروع ، نیمه اول Adder دو ورودی باینری اصلی ، A و B را می گیرد که رقم اصلی اضافه شده است.وظیفه اصلی آن محاسبه مبلغ و حمل اولیه این دو شماره است.در اینجا ، نیمه اول Adder دو نتیجه را ارائه می دهد: یک مبلغ اولیه (SUM1) و یک حمل اولیه (Carry1).Sum1 از عملکرد XOR A و B مشتق شده است ، نشان می دهد که آیا کل تعداد 1 از 1 را دارد یا خیر.Carry1 ، نتیجه و عملکرد بین A و B ، نشان می دهد که آیا هر دو رقم 1 هستند ، که نیاز به حمل به بیت بالاتر بعدی دارد.

در مرحله بعد ، نیمه دوم Adder به این روند می پیوندد.از خروجی SUM1 و سوم ورودی ورودی سوم (حمل از یک محاسبه قبلی) به عنوان ورودی های آن استفاده می کند.نیمه دوم Adder دو خروجی تولید می کند: نتیجه جمع نهایی (SUM2) و حمل ثانویه (Carry2).Sum2 ، که نتیجه XOR Sum1 و CIN است ، مبلغ نهایی سه ورودی را نشان می دهد و علاوه بر این باینری جمع شده را نشان می دهد.Carry2 ، که از عملکرد بین Sum1 و CIN بیرون می آید ، نشانگر حمل تولید شده توسط این مؤلفه ها است.

Full Adder Circuit with Using Two Half Adder

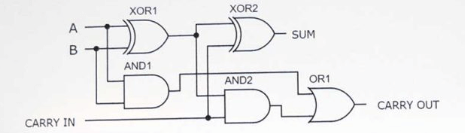
شکل 5: مدار Adder کامل با استفاده از دو نیمی از Adder

سرانجام ، برای تکمیل طراحی کامل Adder ، یک دروازه یا دروازه لازم برای رسیدگی به خروجی های حمل و نقل Carry1 و Carry2 از هر دو اضافه کننده است.این یا دروازه تضمین می کند که هرگونه حمل تولید شده در طول محاسبات به درستی به خروجی نهایی منتقل می شود.بنابراین ، خروجی نهایی ADDER (COUT) نتیجه OR Carry1 و Carry2 است.گنجاندن این یا دروازه تضمین می کند که کلیه حمل های بالقوه به طور دقیق محاسبه و به سطح بعدی در عملیات اضافی چند بیتی منتقل می شوند و از یکپارچگی عملکرد حسابی در چندین بیت اطمینان می دهند.

مزایا و چالش های افزودنی کامل در منطق دیجیتال

افزودنی های کامل نقش مهمی در طراحی منطق دیجیتال دارند و مزایای بی شماری را ارائه می دهند که باعث می شود آنها در سناریوهای مختلف محاسبات و پردازش داده ها ضروری باشند.مزایای اصلی آنها شامل انعطاف پذیری قابل توجه ، سرعت پردازش سریع و مدیریت حمل کارآمد است.این صفات ، افزودنی های کامل را برای اجرای عملیات پیچیده حسابی و توابع منطقی ، به ویژه در برنامه هایی که نیاز به افزودن چند بیتی متوالی دارند ، ایده آل می کند.

مزایا

انعطاف پذیری: افزودنی های کامل در توانایی خود در پردازش چندین ورودی باینری (A ، B و CIN) به طور همزمان برتری دارند.آنها همچنین می توانند به آرایه های بزرگتر برای رسیدگی به شماره های باینری طولانی تر گسترش یابند.این مقیاس پذیری برای ایجاد واحدهای منطق حسابی با کارایی بالا (ALUS) مهم است ، که باید عملیات پیچیده و حسابی و منطقی پیچیده را انجام دهد.

سرعت: به لطف معماری پردازش موازی داخلی آنها ، افزودنی های کامل می توانند افزودن همه ورودی ها را در یک چرخه ساعت واحد انجام دهند و در عین حال تعیین کننده خروجی ها را نیز تعیین می کنند.این قابلیت از عملیات افزودنی مداوم پشتیبانی می کند و برای پردازش داده های زمان واقعی در ریزپردازنده های مدرن و دستگاه های محاسباتی با سرعت بالا ضروری است.

معایب

با این حال ، افزودنی های کامل همچنین مضرات قابل توجهی را ارائه می دهند:

پیچیدگی در طراحی و اجرای: افزودنی های کامل شامل چندین دروازه منطقی و انتشار چند سطحی هستند و طراحی آنها را پیچیده می کنند.این پیچیدگی نه تنها هزینه های تولید را افزایش می دهد بلکه می تواند بر قابلیت اطمینان مدارها نیز تأثیر بگذارد.

مسائل تأخیر در انتشار: انتشار ممکن است از چندین دروازه منطقی عبور کند ، هر کدام تاخیر خود را اضافه می کنند.این می تواند سرعت محاسباتی کلی را در طول عملیات در مقیاس بزرگ ، به ویژه در سیستم های رایانه ای گسترده و در طراحی ادغام در مقیاس بسیار بزرگ (VLSI) و پردازنده های پر سرعت محدود کند.این تأخیر می تواند به یک تنگنا مهم در عملکرد تبدیل شود.

برای کاهش این مسائل ، مهندسان به طور مداوم طرح های مدار کارآمدتر را کشف می کنند.استراتژی ها شامل استفاده از فن آوری های گیت منطقی سریعتر ، بهینه سازی طرح های مدار برای کوتاه کردن طول مسیر و توسعه فن آوری های پیشرفته مانند افزودنی های حمل و نقل برای به حداقل رساندن تأخیرها در انتشار است.

برنامه های کاربردی کامل در منطق دیجیتال

افزودنی های کامل به طور گسترده در منطق دیجیتال مورد استفاده قرار می گیرند ، که برای انعطاف پذیری و کارآیی آنها جایزه می گیرند و آنها را در بسیاری از کارهای محاسباتی و پردازش داده ها محوری می کنند.برنامه کاربردی آنها از عملیات اساسی حسابی گرفته تا پردازش سیگنال پیچیده و کنترل سیستم.در اینجا نگاهی دقیق به برخی از زمینه های کلیدی که افزودنی های کامل در آن یکپارچه هستند ، آورده شده است.

مدارهای حسابی

یکی از ساده ترین کاربردهای افزودنی کامل در مدارهای حسابی است که علاوه بر این باینری را انجام می دهند.به خصوص در علاوه بر تعداد چند بیتی ، افزودنی های کامل توالی های باینری طولانی تر را از طریق آبشار مدیریت می کنند.در این ترتیب ، هر یک از تبلیغات کامل برای موقعیت بیت و حمل از بیت پایین ، علاوه بر این ، حمل جدید را به عنوان کامل بیت بالاتر بعدی منتقل می کند.این آبشار امکان افزودنی جامع چند بیتی را در کل طیف وسیعی از رقم ها فراهم می کند.

داده های پردازش

افزودنی های کامل همچنین نقش مهمی در کارهای پیشرفته پردازش داده ها مانند پردازش سیگنال دیجیتال (DSP) برای فیلتر و تبدیل فوریه دارند ، جایی که به عملیات دقیق و سریع حسابی نیاز است.علاوه بر این ، در حوزه امنیت اطلاعات ، از جمله رمزگذاری داده ها و الگوریتم های تشخیص خطا و تصحیح مانند بررسی های برابری و تولید کد چک افزونگی چرخه ای (CRC) ، افزودنی های کامل برای اجرای عملیات بیت اساسی بسیار مهم هستند.

شمارنده

در پیشخوان های دیجیتال ، افزودنی های کامل برای اجرای هر دو عملکرد افزایش و کاهش ، به ویژه در پیشخوان های مدولار و همزمان ضروری هستند.آنها برای اطمینان از شمارش دقیق ، حمل و وام را به طور دقیق مدیریت می کنند.

Multiplexers (Mux) و demultiplexers (Demux)

در مولتیپلکسرها و demultiplexers ، افزودنی های کامل نقش مهمی در انتخاب کانال و توزیع داده ها دارند.آنها در منطق شرکت می کنند که تعیین می کند کدام کانال ها برای ورودی و خروجی داده ها استفاده می شوند و تصمیم گیری بر اساس سیگنال های کنترل منطقی می گیرند.

فناوری حافظه

در آدرس حافظه ، افزودنی های کامل به تولید سیگنال های آدرس برای دسترسی پویا به مکانهای حافظه کمک می کنند.این امر به ویژه در حافظه دسترسی تصادفی پویا (DRAM) و سایر سیستم های ذخیره سازی ، که در آن افزودنی های کامل از محاسبات آدرس پیچیده برای افزایش کارآیی دسترسی به حافظه پشتیبانی می کنند ، از اهمیت ویژه ای برخوردار است.

واحدهای منطق حسابی (ALU)

سرانجام ، به عنوان مؤلفه های اساسی واحدهای منطق حسابی در ریزپردازنده ها و پردازنده های سیگنال دیجیتال ، افزودنی های کامل بسیار مهم هستند.ALU تمام عملیات حسابی و منطق را انجام می دهد ، و افزودنی های کامل اطمینان حاصل می کنند که داده ها به سرعت و دقیق پردازش می شوند.

نمونه هایی از اجرای کامل Adder

افزودنی های کامل را می توان با استفاده از دروازه ها و تنظیمات مختلف منطق ساخت.در اینجا ، ما چهار پیاده سازی مختلف را کشف می کنیم ، و تفاوت های عملیاتی آنها را برجسته می کنیم.

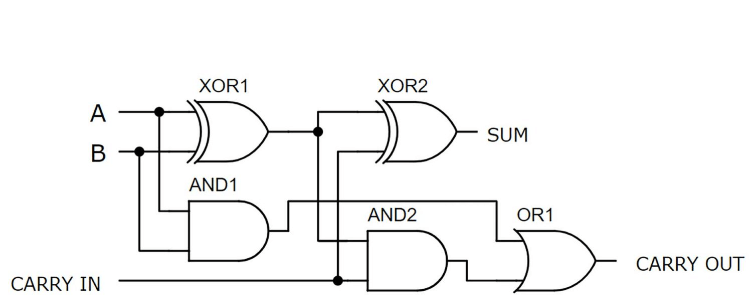
تبلیغ کامل ساخته شده با XOR ، و و یا دروازه

Full Adder Built with XOR, AND, and OR Logic Gates

شکل 6: تبلیغ کامل ساخته شده با دروازه های XOR ، و یا منطق

این مثال یک تبلیغ کامل را که با استفاده از ترانزیستورهای گسسته بر روی یک تخته نان ساخته شده است ، به نمایش می گذارد.پیکربندی شامل پنج دروازه منطقی است: دو دروازه XOR ، دو و دروازه و یک یا دروازه که به 21 ترانزیستور نیاز دارد.ورودی های A و B به سمت چپ بالای تخته وصل می شوند و یک منبع A +5 ولت را دریافت می کنند.این ورودی ها با استفاده از دو سوئیچ ضامن کنترل می شوند.دو LED در سمت چپ بالا حاکی از وضعیت ورودی های A و B است ، در حالی که دو LED در سمت راست خروجی ها را نشان می دهند.مقاومتهای مورد استفاده در مدار همه 2.2 کیلومتر اهم هستند.هنگامی که ورودی های A و B روشن است و حمل آن خاموش است ، خروجی مقدار باینری 10 را نشان می دهد ، که مبلغ 2 را نشان می دهد (1 + 1 + 0 = 10).دروازه های XOR که با 12 ترانزیستور اول ساخته شده است ، جمع بندی اولیه را انجام می دهند ، در حالی که نیمی از قسمت پایین نان حاوی و یا دروازه هایی برای عملیات حمل است ، سیم کشی با کد رنگی وضوح و عیب یابی را تقویت می کند.

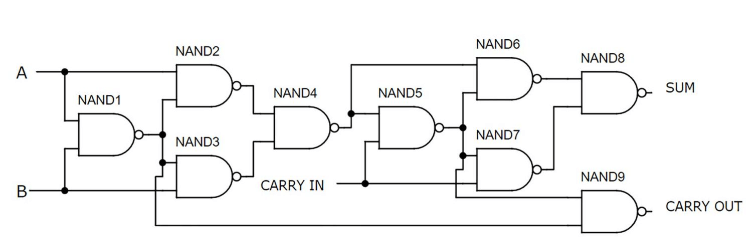
تبلیغ کامل با استفاده از دروازه های NAND

شکل 7: تبلیغ کامل با استفاده از دروازه های NAND

این Adder کامل از نه دروازه NAND استفاده می کند ، با هر دروازه از دو ترانزیستور ، در مجموع 18 ترانزیستور.این روش از ساده ترین و کارآمدترین راهها برای ساخت یک تبلیغ کامل با استفاده از اجزای گسسته است.تمام دروازه ها در نیمه بالایی تخته نان مونتاژ می شوند ، در حالی که سوئیچ ها نیمه پایین را اشغال می کنند.عملکرد مدار با ورودی های A و B ON و Carry-in خاموش نشان داده شده است و در نتیجه مقدار باینری خروجی 10 ، معادل اعشاری 2 است.

تبلیغ کامل با Nor Gates

شکل 8: تبلیغ کامل با NOT GATES

این تنظیم با نه دروازه و NOR که به دو ترانزیستور نیاز دارد ، در کل از 18 ترانزیستور نیز استفاده می کند.ساختن یک تبلیغ کامل با Nor Gates یک جایگزین مناسب ارائه می دهد اما شامل سیم کشی پیچیده تر در مقایسه با دروازه های NAND است.هر ترانزیستور در دروازه های NOR پایه گذاری شده است و جمع کننده ها توسط سیم های بلوز نارنجی برای اطمینان از سیم کشی مرتب و سازمان یافته متصل هستند.این پیکربندی با ورودی های A و B فعال شده و مخزن غیرفعال شده نشان داده شده است و منجر به خروجی هایی می شود که حمل آن فعال است و مبلغ آن خاموش است.

پایان

در طول این اکتشاف از فناوری ADDER ، از نیمی از افزودنی های اصلی گرفته تا طرح های پیشرفته کامل Adder ، بدیهی است که این مؤلفه ها برای پیشرفت الکترونیک دیجیتال بنیادی هستند.ویژگی های عملیاتی و نمونه های اجرای آن ، بر همه کاره بودن و کارآیی افزودنی ها در تنظیمات مختلف محاسباتی تأکید می کنند.با بررسی ساختار و عملکرد افزودنی ها ، به ویژه از طریق جداول حقیقت و معادلات مشخصه آنها ، بینش های ارزشمندی در مورد توانایی ها و محدودیت های آنها کسب می کنیم.این دانش در پیشبرد طراحی سیستم های محاسباتی کارآمدتر و سریعتر مؤثر است.در نهایت ، افزودنی ها نه تنها محاسبات باینری پیچیده را ساده می کنند بلکه باعث گسترش تکنولوژی در مناطقی می شوند که به اندازه پردازش داده ها ، تخصیص حافظه و پردازش سیگنال دیجیتال متنوع هستند.با تکامل فناوری دیجیتال ، پالایش و نوآوری مداوم در طراحی ADDER همچنان به عنوان سنگ بنای توسعه معماری های محاسباتی پیشرفته تر خواهد بود و اطمینان حاصل می کند که این اجزای اساسی در قلب طراحی و اجرای سیستم دیجیتال باقی می مانند.

سوالات متداول [سؤالات متداول]

1. مدار تبلیغاتی کامل چیست؟

یک Adder کامل یک مدار دیجیتالی است که سه بیت باینری را برای تولید یک مبلغ و یک خروجی حمل اضافه می کند.این طراحی برای رسیدگی به سه ورودی طراحی شده است: دو بیت مهم و یک بیت حمل و نقل از یک افزودنی قبلی.این اجازه می دهد تا در مراحل پی در پی برای اضافه کردن اعداد باینری چند بیتی استفاده شود.

2. چند و ، یا ، یا xor در تبلیغ کامل؟

یک تبلیغ کامل معمولی شامل:

دو دروازه XOR برای تولید مبلغ.

دو و دروازه برای کمک به محاسبه حمل.

یک یا دروازه برای نهایی کردن خروجی حمل.

3. ورودی حمل در Adder کامل چیست؟

ورودی Carry (CIN) در یک افزودنی کامل ، بیت حمل از افزودن بیت های قابل توجه پایین قبلی در افزودنی باینری چند بیتی است.این امکان را به شما می دهد تا هنگام محاسبه مبلغ فعلی و حمل جدید ، این حمل قبلی را در نظر بگیرد.

4- چرا از یک تبلیغ کامل به جای نیمی از تبلیغ استفاده می کنید؟

از یک تبلیغ کامل به جای یک نیمی از تبلیغ استفاده می شود زیرا می تواند سه بیت (از جمله حمل اضافی از افزودنی های قبلی) اضافه کند ، و این باعث می شود که برای اضافه کردن شماره های چند بیتی ، برای زنجیر کردن مناسب باشد.یک آدرید نیمه فقط می تواند دو بیت اضافه کند و برای حمل و نقل تأمین نمی کند ، که استفاده از آن را به ساده ترین اشکال اضافه کردن باینری بدون انتشار حمل پی در پی محدود می کند.

دربارهی ما

ALLELCO LIMITED

Allelco یک توقف بین المللی مشهور است توزیع کننده خدمات تهیه کننده اجزای الکترونیکی ترکیبی ، متعهد به ارائه خدمات جامع و خدمات زنجیره تأمین برای صنایع جهانی تولید و توزیع الکترونیکی ، از جمله 500 کارخانه برتر OEM و کارگزاران مستقل.
ادامه مطلب